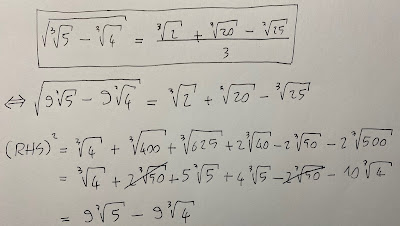La Quinta aurea

Fra i brani spesso menzionati in relazione alla sezione aurea c'è pure la Quinta Sinfonia di Ludwig van Beethoven, citata e stracitata pure nella musica leggera. Le prime cinque battute dell'introduzione (il destino che bussa alla porta) sono ormai leggenda:

 

Come fece notare nel 1978 il didatta della matematica Derek Haylock (in un articolo difficile da reperire, ma essenzialmente replicato qui), nella partitura originale il primo movimento della Sinfonia consiste di 600 battute, e alla 372-esima ritroviamo una ripetizione dell'incipit. I rapporti 600:372 e ancora di più (applicando il trucchetto rivelato qui) 972:600 forniscono approssimazioni abbastanza precise del valore di phi. 

Caso o calcolo? A dire il vero non farebbe una grande differenza. 

Ascoltiamocela, però, in quella che viene da alcuni considerata la migliore interpretazione di sempre, eseguita nel 1974 dai Wiener con la bacchetta di Carlos Kleiber:

Altre letture…

Tre libri, che hanno, anche solo marginalmente, a che fare con la matematica (i numeri 57, 64 e 65 di questo 2021 ricco di letture, non proprio tutte tutte edificanti, però).

• Dall’improbabile all’infinito, di Edward B. Burger e Michael Starbird. Il sottotitolo, Caos, coincidenze e altre sorprese matematiche, descrive fedelmente quello che ci si può aspettare dal libro. In particolare, ci troviamo tutta una serie di argomenti resi popolari dalla divulgazione matematica: in ordine sparso, la crittografia, la sezione aurea e i numeri di Fibonacci, il concetto di dimensione, l’ipercubo, l’Hotel Hilbert, il caos, la serie armonica, il nastro di Möbius, … Ho particolarmente apprezzato, perché ho imparato qualcosa di nuovo, il capitolo dedicato agli Origami, che dalla semplice piegatura di un nastro di carta ci conduce su, su fino alla curva del drago e quindi alla geometria frattale, e perfino alla macchina di Turing. Il volume è pensato per i non-specialisti, e quindi mantiene un livello di approfondimento moderato. Mi sento davvero di consigliarlo.
• Un po' meno consigliabile, a mio avviso, è Quando abbiamo smesso di capire il mondo, di Benjamin Labatut. Gli eroi di questo libro sono alcuni tra i personaggi, nel bene e nel male, più interessanti della scienza del XX (e XXI, in parte) secolo: Fritz Haber, Karl Schwarzschild, Werner Heisenberg, Erwin Schrödinger. E, soprattutto, Alexander Grothendieck e Shinichi Mochizuki. Ed è soprattutto la presenza di questi ultimi ad avermi convinto ad acquistare e leggere il libro. Man mano che proseguivo nella lettura, però, ho avvertito la sensazione crescente che qualcosa non mi quadrasse. E, in effetti, al capitolo "Ringraziamenti" l'autore ci rivela che "la quantità di finzione va aumentando nel corso del libro", e che, in particolare, la biografia di Mochizuchi è inventata di sana pianta (certo, sarebbe stato commovente se al capezzale di Grothendieck ci fosse stato lui, un po' meno se in seguito il matematico giapponese avesse davvero tentato di dar fuoco alla biblioteca dell'Università di Montpellier). Alcune delle invenzioni, poi, mi sembrano di gusto non proprio ottimo, tipo i deliri mistico/erotici di Heisenberg nella notte di Helgoland.
  In sintesi, ma ovviamente si tratta della personalissima opinione di un non-letterato, un'opera in bilico tra biografia e fiction (ma sbilanciata su quest'ultima), di cui francamente fatico a comprendere a fondo le finalità. 
• I geni della creatività, di Simon Baron-Cohen (il cugino di Borat - sì, per davvero). L'ho letto perché Michele Emmer ne parlava qui, e mi ha incuriosito. Baron-Cohen, un'autorità nello studio dei disturbi dello spettro autistico, identifica nel "meccanismo di sintetizzazione" (l'identificazione degli schemi che lui definisce "se-allora") la capacità di far fronte alle nuove sfide che ha guidato l'evoluzione del genere umano. Bilanciando la capacità di sistematizzare con l'empatia, Baron-Cohen identifica cinque tipologie di cervello, dal "tipo S estremo" dei super-sistematizzatori (alla Edison) al "tipo E estremo" di chi è, ad esempio, totalmente refrattario alle nuove tecnologie ma insuperabile nella gestione dei rapporti umani.
  Ovviamente, il "tipo S" (anche piuttosto estremo), fa spesso capolino, almeno secondo la mia esperienza, all'interno dei dipartimenti di matematica...
  

Geometria vintage

Un annetto e mezzo fa (sembrava un’altra epoca), un paio di settimane prima che il mondo precipitasse nel caos pandemico, da un antiquario vicino alla Galleria degli Uffizi ho acquistato, quasi per caso, un volumetto di geometria vecchio di quasi duecent’anni (l’antiquariato librario suscita sempre la mia curiosità). Si tratta delle Instituzioni delle sezioni coniche ordite dal sacerdote D. Felice Giannattasio, pubblicato a Napoli nel 1830. In stile perfettamente euclideo, il Giannattasio propone una rigorosa costruzione delle sezioni coniche, preceduta da una dotta introduzione storica. Il trattato, che non ho avuto il coraggio di leggere nei dettagli, è costituito da uno stillicidio di assiomi che, passo dopo passo, conducono ai ben noti risultati su ellisse, iperbole e parabola. Ad esempio, la proposizione XXVI consiste nella celebre definizione del giardiniere dell’ellisse:

La trattazione delle coniche a livello liceale, oggi (sempre che le si tratti, cosa a mio avviso non indispensabile) avviene con linguaggi e metodi diversi, tra l’altro già disponibili nel 1830. Innanzitutto si fa uso della geometria analitica, che Giannattasio mostra peraltro di conoscere:

E, soprattutto, le definizioni piane vengono derivate dalle intersezioni di un piano e un cono per mezzo delle geniali intuizioni di Pierre de Dandelin (pubblicate nel 1822), le cui sfere permettono una transizione del tutto naturale dallo spazio tridimensionale al piano.

Curiosando qua e là nel libro, mi sono imbattuto in un piccolo risultato di geometria piana che per qualche motivo ha risvegliato la mia curiosità:

Giannattasio lo dimostra facendo uso di due proposizioni degli Elementi che, essenzialmente, rappresentano dei precursori del Teorema del coseno (noto in Italia anche come Teorema di Carnot):

 

Utilizzando le potenti tecniche messe a disposizione dal Delle Carte potremmo anche argomentare come segue:

Qualche notizia biografica sul Giannattasio la si può trovare qui, sul sito dedicato ai più illustri cittadini di Solofra, in provincia di Avellino. Vi si trova pure un sonetto a lui dedicato, composto da un altro Solofrano illustre, il sacerdote Carmine Troisi:

Il matematico 

Felice Giannattasio, figlio mio,

era un valore nelle scienze esatte,

e, al tempo stesso, un ministro di Dio,

d'indole poi tutta miele e latte;

semplice e schietto inoltre, come un rio

che serpeggiando vada tra le fratte,

di cui, pur fioco essendo il mormorio,

ogni seme feconda in cui s'imbatte.

Era anche un uom di spirito e frugale,

sì che spesso un bel cavolo fumava

sul suo rude ma candido mensale,

un cavolo che lui stesso comprava,

condendol poi con dell'olio e sale,

appunto come, al secol d'òr, s'usava.

Un Mozart aureo?

 

Sono stati in molti, l'ho già scritto, a scandagliare la musica per mezzo della sezione aurea, o addirittura a utilizzarla esplicitamente all'interno delle composizioni (vedi ad es. qui e qui). Nel suo articolo The Golden Section and the piano Sonatas of Mozart (leggibile qui; JSTOR non permette lo scaricamento, ma concede 100 visualizzazioni mensili gratuite), il matematico e insegnante statunitense John Putz prende in esame alcune Sonate per pianoforte del genio salisburghese, indagando il rapporto numerico tra le durate della prima parte (l'esposizione), di durata $a$, e la seconda (sviluppo e ricapitolazione), di durata $b$. Un grafico a dispersione (scatter plot) delle variabili $a$ e $b$ rivela un'intrigante regolarità:

Tale regolarità sembra ancor più evidente utilizzando le variabili $b$ e $a+b$:

In entrambi i casi, la crescita sembra piuttosto lineare, e una semplice regressione rivela un coefficiente angolare molto vicino a $\varphi=\frac{1}{\phi}=1-\phi \cong 0.62$ (nel primo caso $0.6260$, nel secondo $0.6091$). Sembrerebbe quindi che Mozart, che una certa propensione per la matematica effettivamente l'aveva, abbia più o meno consapevolmente abbellito alcune sue composizioni impiegando la sezione aurea. Ma è lo stesso Putz a metterci in guardia, da un lato mostrandoci come vincoli ragionevoli sulle durate $a$ e $b$ non conducano lontano da $\frac{a}{b}=\varphi$, dall'altro insegnandoci come "barare" per mezzo della relazione, valida se $0\le a \le b$,
$$
\left| \frac{b}{a+b}-\varphi \right| \le \left| \frac{a}{b}-\varphi \right|
$$

che ci suggerisce che, per convincere il pubblico del fatto che il rapporto tra due grandezze $a$ e $b$ è aureo, converrà sempre esibire $\frac{b}{a+b}$ piuttosto che $\frac{a}{b}$.
 

Lo zio Giuseppe

... ossia Giuseppe Peano, zio, anzi prozio, di Lalla Romano, fa la sua comparsa nel "romanzo di formazione" Una giovinezza inventata, dove l'autrice descrive la sua malinconica educazione sentimentale e artistica nella Torino degli anni '20. L'ho appena terminato; è un po' lontano dalle mie letture abituali, e quindi non credo di avere gli strumenti per parlarne con cognizione di causa.
Sono un po' più a mio agio, invece, con il fascicoletto Giochi di aritmetica e problemi interessanti, che ho acquistato a un'asta online (ma che si può scaricare, in una riedizione Sansoni uscita una quarantina di anni fa, a questo indirizzo). Pubblicato nel 1923, e destinato agli insegnanti delle scuole elementari, contiene una collezione di problemini, da cui traspaiono qua e là l'arguzia e la cultura del matematico e glottoteta torinese, figura fondamentale della matematica a cavallo tra XIX e XX secolo, i cui assiomi per la definizione dei numeri naturali fanno spesso capolino anche all'interno dei percorsi liceali. 

Alcuni dei problemi posti sono dei veri e propri evergreen, ad esempio

oppure anche il meno elementare

(reso popolare da Lewis Carroll), e anche il celebre

 

 

Interessante (e lapidaria) è infine la conclusione, che mostra come lo zio Giuseppe avesse a cuore la qualità dell'insegnamento, fin dal livello più basso (e, nel contempo, anche il benessere dell'insegnante):

Qualche libro, per ricominciare...

È strano... Dopo un finale di anno scolastico come sempre abbastanza intenso, mi ero riproposto di dedicarmi a questo blog nel corso dell'estate. E invece devo confessare di essermi piuttosto disinteressato della matematica, almeno fino al momento di iniziare a preparare i (numerosi) corsi che mi aspettano quest'anno, dove tra l'altro le novità non sono poche (nuovo piano degli studi...). Ho letto, sì, anche parecchio, ma soprattutto narrativa, diciamo così, d'evasione. Perché forse di evadere un po' ne avevo bisogno.
Ho comunque tre libri che stazionano da tempo, nell'attesa di essere (almeno sommariamente) recensiti. Ne parlo in breve, così da poterli finalmente riporre. 

• Le equazioni del cuore, della pioggia e delle vele, di Alfio Quarteroni. Le due vittorie del Team Alinghi nell'America's Cup riuscirono ad appassionare alla vela una nazione non propriamente marinara come la Svizzera (purtroppo la terza partecipazione, contraddistinta da un estenuante preludio di carattere legale e da scafi di concezione molto diversa, andò male), e diedero una certa notorietà anche al responsabile del team che si occupò delle simulazioni numeriche nella progettazione degli scafi, appunto Quarteroni (definito per un po' il "matematico di Alinghi"). Ricordo, tra l'altro, una sua appassionante conferenza al liceo di Locarno, e una graditissima visita ai nostri studenti luganesi.
  Il volumetto, edito da Zanichelli, propone, senza addentrarsi troppo nelle questioni più tecniche, una scelta di spettacolari applicazioni del calcolo scientifico: la tradizionale metereologia, l'epidemiologia (tristemente attuale...), la simulazione dei flussi sanguigni e la navigazione terrestre (Alinghi, appunto) e atmosferica (con il progetto Solar Impulse). Una lettura decisamente consigliata, perché ci mostra come la matematica trovi oggi (massicciamente) posto in ambiti inattesi, contribuendo al progresso tecnologico anche nel salvare (molte) vite umane.
  
• Racconto matematico, di Michele Emmer. Matematico, regista, saggista e divulgatore, Emmer ci propone un viaggio che, tra matematica, letteratura, teatro, cinema e arti figurative, a un certo punto ci conduce addirittura dentro la testa dei matematici. Per definire l'opera di Emmer, non me la sentirei di usare il termine divulgazione; qui siamo decisamente a un livello più alto. Si tratta di un saggio dal valore culturale notevole, da cui partire per scoprire aspetti nuovi e inattesi della materia che ci sta tanto a cuore. Mi ha permesso di riflettere anche su qualche aspetto del mio carattere, anche se non rivelerò in che modo...
  
• The theory that would not die. How Bayes' rule cracked the Enigma code, hunted down russian submarines & emerged triumphant from two centuries of controversy (un titolo che è tutto un programma), di Sharon Bertsch McGrayne. La statistica non è mai stata il mio campo d'azione preferito, e quindi ho sempre faticato un po' a comprendere a fondo tutti i retroscena della diatriba tra bayesiani e frequentisti. Nel saggio in questione, molto completo e documentato, la giornalista scientifica Sharon Bertsch McGrayne si schiera dalla parte di Thomas Bayes, facendo luce sul ruolo determinante della sua "regola", che essenzialmente consiste nell'aggiornare la propria convinzione sulla base dei dati acquisiti successivamente. Tra i numerosi esempi d'applicazione sviscerati nel testo, ho trovato particolarmente interessante la ricerca degli autori dei Federalist Papers, che mi ha ispirato a sfogliare anche il volume Applied Bayesian and Classical Inference. The case of "The Federalist" papers, di Frederick Mosteller e David L. Wallace. Forse prima o poi ne parlerò anche qui.

Da semplici a impossibili

Per qualche motivo, nel corso del periodo Edo della storia giapponese (1603-1868) vigeva la curiosa usanza di esporre, nei templi buddisti o shintoisti, tavolette votive a tema geometrico. Si trattava dei cosiddetti Sangaku (算額), che consistevano di problemi o teoremi illustrati su tavole di legno, spesso incentrati sulle proprietà delle circonferenze. Alcuni di essi sono facilmente proponibili anche alle prime classi liceali (o forse anche più presto), come i seguenti due, dove si tratta di ricavare la relazione tra i raggi di tre circonferenze tangenti tra loro e a una stessa retta e il raggio del cerchio inscritto tra il quadrato e i due quarti di circonferenza.

Praticamente tutti i Sangaku "sopravvissuti" sono stati risolti o discussi; la stragrande maggioranza di essi richiede soltanto qualche competenza elementare. Fanno eccezione almeno due problemi, discussi in un paio di recenti pubblicazioni. Il primo, la cui irrisolvibilità in termini algebrici viene discussa qui con tecniche che si spingono fino alla teoria di Galois, rimpiazza essenzialmente il circolino del quesito ritratto sopra a sinistra con il più grande quadrato possibile. Il secondo, tratto dal Diario di viaggio di Yamaguchi Kanzan, discusso qui, riguarda tre cerchi inscritti tra un'ellisse e un triangolo rettangolo, e conduce a equazioni a dir poco mostruose. Il paper di Hisoshi Kinoshita contiene però anche un Lemma carino sull'inscrivibilità di due cerchi in un'ellisse, che non mancherò di infliggere a qualche mia classe.

Tra l'altro, ai Sangaku è dedicato anche un periodico online ad accesso libero,  il Sangaku Mathematical Journal, che sembra contenere parecchia matematica elementare interessante.

Rombotriesagonale

... cioè formata da esagoni, contornati da quadrati e triangoli equilateri. È la tassellazione che ricopre parte del pavimento del Battistero paleocristiano di Riva San Vitale (probabilmente originale, e forse risalente a un precedente edificio di epoca romana), il più antico monumento cristiano presente su suolo svizzero (V-VI sec.), che ho brevemente visitato qualche giorno fa (in questo periodo, ci tocca accontentarci delle attrazioni turistiche locali). Si tratta di una delle otto tassellazioni archimedee o semiregolari (semi- perché coinvolgono più di un tipo di poligoni, in questo caso tre), denotata dal Simbolo di Schläfli rr{6,3} (nella notazione „orizzontale“ abbreviata di Norman Johnson), una doppia rettificazione (o cantellazione) di una tassellazione esagonale {6,3} (un alveare).

Per cercare di capire il senso del Simbolo di Schläfli in questo contesto, mentre i miei allievi di prima si esercitavano sui polinomi di II grado, ho fatto distrattamente uno schizzo delle due rettificazioni, da {6,3} a rr{6,3} passando per r{6,3}, la tassellazione triesagonale. Eccolo:

Qualcosina non mi quadra ancora (nella forma dei rettangoli, che nel pavimento sono dei quadrati). Ma suppongo che i simboli di Schläfli (argomento su cui non sono particolarmente ferrato) esprimano la topologia della situazione (e quindi non tengano conto di eventuali deformazioni).

Buonpigiorno!

Per ovvie ragioni, il 14 marzo (3.14 negli USA) è oramai diventato il "$\pi$-day". Sembra che l'idea sia venuta inizialmente al fisico Larry Shaw, per 33 anni attivo all'Exploratorium di San Francisco, dove la ricorrenza viene sottolineata tutti gli anni da una serie di eventi.

Assieme a $\phi$, $\sqrt{2}$ e a $e$, $\pi$ è senz'altro il più noto numero irrazionale. Fu Johann Heinrich Lambert, nel 1761, il primo a dimostrarlo, facendo uso di uno sviluppo della funzione $\tan(x)$ come frazione continua. Da allora in molti hanno presentato dimostrazioni alternative, spesso più semplici. Fra le più carine c'è quella pubblicata da Ivan Niven nel 1947 sul Bulletin of the AMS. Eccola, ci sta tutta qui:

Tra l'altro, la stessa dimostrazione (più o meno) è data per esercizio nel fondamentale Fonctions d'une variable réelle, il volume dedicato dal gruppo Bourbaki ai rudimenti dell'analisi:

A4 e la radice di due

$21 \times 29.7$ ${\rm cm}$. Era più o meno tutto quello che ricordavo dei "fogli A4", forse dai tempi delle lezioni di "Educazione Tecnica" in III media (quando, in contemporanea, le ragazze seguivano ancora il corso di "Lavoro femminile"; altri tempi...). Fino a quando sono inciampato su un esercizio attribuito da un collega, in cui lo standard dei fogli A0, A1, A2 ecc. veniva definito più o meno così:

• la superficie del foglio A0 misura 1 ${\rm m}^2$;
• piegando a metà un foglio An si ottiene il foglio A(n+1), le cui proporzioni rimangono inalterate.

Decisamente più interessante. In effetti, denotando con $a_n$ e $b_n$ i lati (minore e maggiore) del rettangolo An, dalle relazioni tra essi ricaviamo
$$
\begin{cases}
a_0 \cdot b_0 = 1\\
\displaystyle\frac{b_1}{a_1}=\frac{b_0}{a_0}
\end{cases}
$$
e quindi, dato che $b_1=a_0$ e $a_1=\frac12b_0$,
$$
\frac{b_0}{a_0}=\frac{b_1}{a_1}=\frac{a_0}{\frac12b_0}\qquad\iff\quad \left(\frac{b_0}{a_0}\right)^2=2 \;.
$$
Già, il rapporto tra altezza e base (e quindi tra i successivi $a_i$ e $b_i$) è pari a $\sqrt2$. In particolare, da $b_0=\sqrt2 \, a_0=\frac{1}{a_0}$ ricaviamo
$$
a_0=\frac{1}{\sqrt[4]{2}}\quad,\quad a_4=\frac{a_0}{(\sqrt{2})^4}=\frac{1}{4\sqrt[4]{2}}\cong 0.210 \quad\text{e}\quad b_4=\sqrt{2}\,a_4\cong0.297 \quad.
$$
A quanto pare, il primo a rendersi conto dei vantaggi dell'utilizzo di un rapporto pari a $\sqrt{2}$ fu, nel XVIII secolo, il fisico tedesco Georg C. Lichtenberg. Ma fu Lazare Carnot, nel periodo rivoluzionario, a proporre di ufficializzare i formati che sarebbero poi evoluti dapprima nello standard tedesco DIN 476, e poi successivamente nell'ISO 216.

Ma non ci accontentiamo di fermarci qui. Evidentemente, il rapporto $\frac{b_n}{a_n}$ fornisce una successione di approssimazioni razionali della radice di due (vedi anche qui)
$$
\sqrt{2}\cong 1.41421356723730950488 \quad.
$$
Ad esempio, per il foglio A4 vale
$$
\frac{b_4}{a_4}=\frac{297}{210}=\fbox{$\frac{99}{70}$}=1.4\overline{142857} \quad.
$$
Partendo da A0, dalle misure "ufficiali" si ottiene la successione
$$
\frac{b_0}{a_0}=\frac{1189}{841}=\fbox{$\frac{41}{29}$}\;;\;
\frac{b_1}{a_1}=\frac{841}{594}\;;\;
\frac{b_2}{a_2}=\frac{594}{420}=\fbox{$\frac{99}{70}$}\;;\;
\frac{b_3}{a_3}=\frac{594}{420}=\frac{140}{99}\;.
$$
Per curiosità, ho provato a confrontare tali rapporti con le approssimazioni razionali ottenute dai convergenti dello sviluppo di $\sqrt{2}$ come frazione continua. Innanzitutto, da
$$
\sqrt{2}=1+(\sqrt{2}-1)=1+\frac{1}{1+\sqrt{2}}=1+\frac{1}{2+(\sqrt{2}-1)}=1+\frac{1}{2+\frac{1}{1+\sqrt{2}}}
$$
segue che
$$
\sqrt{2}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+\frac{1}{2+\ldots}}}}=[1;2,2,2,2,\ldots]=[1;\overline{2}] \quad.
$$
I primi convergenti, cioè le approssimazioni razionali ottenute troncando la frazione continua, sono
$$
c_0=1\;;\;c_1=\frac{3}{2}\;;\;c_2=\frac{7}{5}\;;\;c_3=\frac{17}{12}\;;\;c_4=\fbox{$\frac{41}{29}$}\;;\;c_5=\fbox{$\frac{99}{70}$} \;.
$$
Cioè: le approssimazioni ottenute dai fogli A0, A2 e A4 sono migliori approssimazioni razionali (non migliorabili, cioè, con frazioni dal denominatore più piccolo).

Seezza & Quasità

 

Alan Moore non è stato l'unico fumettaro a farsi affascinare dalle "dimensioni aggiuntive". Leggendo la nuova edizione degli Incubi di provincia, raccolta di brevi storie "di nicchia" di quel geniaccio del fumetto che è stato Franco Bonvicini alias Bonvi (ricordate? Le Sturmtruppen, Nick Carter, le Cronache del dopobomba, le Storie dello spazio profondo, Cattivik, Marzolino Tarantola) mi sono imbattuto nel racconto Seezza della Quasità, dove il fortuito ripiegamento di una sorta di origami (come quello della casa nuova di Heinlein) origina uno squarcio nello spaziotempo che avrà conseguenze inimmaginabili per l'intero genere umano. Seezza e Quasità sono i nomi attribuiti alla quarta e alla quinta dimensione, dopo altezza, lunghezza e larghezza.
Bonvi attribuisce l'idea originale a un certo W. S. Trevis, di cui inizialmente non ho trovato traccia online. In realtà si tratta di Walter Stone Tevis, autore americano il cui romanzo forse più famoso, The Queen's Gambit è stato recentemente (ben) trasposto da Netflix nella miniserie La regina degli scacchi (ma ha scritto pure L'uomo che cadde sulla terra,  Lo spaccone e il seguito Il colore dei soldi). Del racconto originale, The Ifth of Oofth, pubblicato nell'aprile del 1957 su Galaxy Science Fiction, Bonvi mantiene l'idea originale, in un'ambientazione un po' più "calda", dove gli insipidi protagonisti sono rimpiazzati dal biondo alter ego dell'autore e dall'Enrichetta, anzi Giovanna, di turno.

Che c'entra il 239?

Anche questa l'ho (ri-)scoperta su Mathematical Constants, Vol. 1:
$$
4\,{\rm arctan}\left(\frac{1}{5}\right)-{\rm arctan}\left(\frac{1}{239}\right)=\frac{\pi}{4}\;.
$$
La verifica, come dicono gli inglesi, è straightforward: essenzialmente, è sufficiente applicare tre volte la formula di addizione per la tangente "rivoltata":

Si tratta della formula che John Machin utilizzò per calcolare le prime cento cifre di $\pi$, sfruttando lo sviluppo in serie di potenza dell'arcotangente (qualche informazione supplementare può essere trovata a questo link).

Ma come avrà fatto?

Sfogliando distrattamente, durante una riunione in MS Teams, il primo volume di Mathematical Constants di Steven Finch, mi sono imbattuto nel denesting (simpatica espressione) di Srinivasa Ramanujan
$$
\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}=\frac{1}{3}\left( \sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}\right) \;.
$$
La verifica è presto fatta:

Ma come cavolo ci sarà mai arrivato? Ah già, dimenticavo, Namagiri...

La semplificazione dei radicali doppi riveste una certa importanza nell'ambito degli algoritmi per il calcolo simbolico, come fa notare Susan Landau nel saggio Simplification of nested radicals (consultabile qui), dove il problema viene trattato, dal punto di vista algebrico e da quello computazionale, con gli strumenti della Teoria di Galois. Con carta e penna, la questione è tutt'altro che abbordabile, dal momento che non esistono metodi generali per il denesting, ma solo qualche algoritmo ad hoc come quelli raccolti qui da Stan Brown.

Fisica, moderna ma già vintage

Come sappiamo, Albert Einstein sviluppò le sue rivoluzionarie teorie soprattutto nei primi decenni del XX secolo. In particolare (ma assolutamente non solo), la Relatività ristretta vide la luce nel corso dell'annus mirabilis 1905, mentre i fondamenti della Relatività generale furono sviluppati tra il 1907 e il 1915.
Risalgono già a quegli anni i primi, pionieristici tentativi di popolarizzare una teoria che decisamente cozzava con la percezione "newtoniana" dell'universo, con i suoi paradossi, la dilatazione del tempo, la luce che si incurva in prossimità delle stelle.
Anche la nascente industria cinematografica iniziava allora ad esplorare la possibilità di dare il suo contributo all'ampliamento della cultura scientifica, con i primi, pionieristici tentativi di sfruttare "effetti speciali" e animazione per raggiungere un pubblico più vasto di quello che si documentava sui libri.
Fu, nel 1922, il cineasta tedesco Hanns Walter Kornblum il primo a produrre un documentario dedicato alla fisica di Einstein. Intitolato  Die Grundlagen der Einsteinschen Relativitätstheorie, fu presentato alla Fiera di Francoforte, con un buon successo di pubblico. Il film, come moltissime altre opere dell'epoca, è purtroppo andato perso; se ne trova però una descrizione abbastanza dettagliata in un paper pubblicato nel 2009 dalla storica della scienza Milena Wazeck, scaricabile da questo link. Parte di esso sopravvive inoltre all'interno di un altra fondamentale opera dell'epoca, The Einstein Theory of Relativity, cortometraggio prodotto nel 1923 dagli studi di animazione Fleischer (celebri per Betty Boop, Popeye e per la prima versione animata di Superman), in collaborazione con Garrett Putnam Serviss, astronomo e pioniere della divulgazione scientifica (nonché autore di SF). Il film accompagnò l'uscita dell'omonimo libro di Serviss, scansionato e leggibile a questo indirizzo.

Ma eccolo, il film. Un vero e proprio tuffo nel passato, in un'epoca in cui i miei nonni erano bambini o poco più. Fa di sicuro un certo effetto pensarci...

Addiator

 

Qualche giorno fa, mentre mi aggiravo all'interno del mercatino Caritas di Giubiasco, l'occhio mi è caduto su uno strano aggeggio color ottone che faceva capolino da una vetrinetta, seminascosto tra pezzi sparsi di argenteria e di bigiotteria, il cui aspetto faceva pensare ad un obsoleto strumento di calcolo. Dopo averci dato un'occhiata, da acquistatore compulsivo quale sono, non ho potuto fare a meno di impossessarmene. Si trattava di un Addiator, cioè di un semplice aritmografo, uno strumento meccanico che permette di eseguire somme (da un lato) e sottrazioni (dall'altro), con un sistema ingegnosamente semplice di cremagliere che permette una gestione semi-automatica dei riporti. Prodotto per oltre un secolo dalla Addiator-Gesellschaft di Berlino, la sua economicita ne decretò un ampio successo di vendita, fino all'avvento delle moderne calcolatrici elettroniche.

Altre letture...

Ultimamente ho letto parecchio. E parecchio di ciò che ho letto aveva più o meno a che fare con la matematica. Ecco i libri numero 50, 55, 57, 58, 60, 61 e 64 di questo 2020 da dimenticare:

Pitagora, il padre di tutti i teoremi, di Umberto Bottazzini. Con la competenza e l'ironia che lo contraddistinguono, Bottazzini ci conduce attraverso un breve viaggio nel mondo del Teorema per antonomasia. Un libro breve e veloce, in linea con le altre uscite della collana Formule dell'editrice Il Mulino. Consigliato, ma chi vuole saperne (ancora) di più può anche dare un'occhiata a questo.

Archimede, il matematico che conquistò Roma, di Francesco Grasso. Il due volte vincitore del Premio Urania Francesco Grasso, noto anche per i suoi romanzi storici, imbastisce una trama credibile sugli ultimi mesi di vita del Genio Siracusano, narrati da un suo fedele servitore e collaboratore, intrecciando con mestiere vicende umane e politiche sullo sfondo della seconda guerra punica (quella degli elefanti di Annibale). Non essenziale, ma si può leggere.

Processo al Pi Greco, di Matt Parker. Jet regalati con punti premio, per finta ma senza calcolarne davvero il valore, catastrofi causate da progetti modificati senza rifare i calcoli, apparecchi radioterapici che diventano letali per un banale errore di programmazione, aerei che partono con il serbatoio mezzo vuoto per una confusione tra libbre e chilogrammi. Il libro di Parker è un vero e proprio campionario di errori (e orrori) imputabili alla dabbenaggine e alla superficialità umana. Decisamente illuminante.

1+1 non fa (sempre) 2, di John D. Barrow. L'ultimo (sì, purtroppo davvero l'ultimo) libro di Barrow, uscito in anteprima mondiale nella collana Intersezioni, rappresenta un breve viaggio nel mondo dei numeri. Partendo dai modi in cui possiamo definirli e rappresentarli, l'autore ci presenta poi, in modo sommario ma convincente,  quattro argomenti tutt'altro che scontati in un libro di divulgazione: la dimostrazione che 1+1 fa davvero 2 (sì, davvero: è tosta, tant'è vero che nei Principia Mathematica è preceduta da centinaia di pagine di fittissima teoria), l'aritmetica transfinita, l'incompletezza e la legge di Benford. Per terminare in modo più filosofico, con un capitolo dedicato a quella che è, a parere dell'autore, l'essenza stessa della matematica.   

La funzione del mondo, di Alessandro Bilotta (testi) e Dario Grillotti (disegni). Anche non conoscendone a fondo le opere ci sono tre cose che ricordo di Vito Volterra: come matematico, è stato uno dei fondatori dell'analisi funzionale e un pioniere nell'applicazione della matematica alle scienze biologiche, e come personaggio pubblico fu tra i pochissimi accademici (12 su 1250) a rifiutarsi di giurare fedeltà al regime fascista. La graphic novel (perché pare che dire il fumetto sia riduttivo) di Bilotta (pluripremiato fumettista italiano, tra gli autori di punta di casa Bonelli) e Grillotti (il cui tratto evocativo ben si adatta a un'opera di questo tipo), da leggere magari come antipasto al libro di Guerraggio e Paoloni, ci presenta una breve biografia del grande uomo di scienza, documentata, delicata e rispettosa, che si spera possa riportare all'attenzione del grande pubblico una figura forse colpevolmente un po' dimenticata.

L'incantatrice dei numeri, di Jennifer Chiaverini. Augusta Ada King, contessa di Lovelace, nata Byron, rappresenta certamente una delle figure più affascinanti della storia della scienza, e la sua vita merita senz'altro di essere raccontata più volte. Ma non sono sicuro che un romanzetto come questo le renda veramente giustizia. Scritto in prima persona, come una sorta di autobiografia, il libro è certamente ben documentato, ma deboluccio per quanto riguarda gli aspetti scientifici, e forse per questo mi ha lasciato abbastanza insoddisfatto. Ma descrive piuttosto bene l'ambiente in cui si mosse Ada, e l'influenza sulla sua attività scientifica di alcune figure fondamentali della scienza del XIX secolo, come Charles Babbage (ovviamente) e la "regina delle scienze" Mary Somerville.

Purtroppo la prematura scomparsa di Ada Lovelace non le permise di portare a compimento il suo percorso scientifico. Anche il suo vero contributo allo sviluppo delle idee di Babbage sulla macchina analitica è abbastanza controverso; ad ogni modo, la sua traduzione annotata dell'articolo di Luigi Menabrea viene considerata fondamentale; in particolare, la nota G, sul calcolo dei numeri di Bernoulli contiene quello che molti considerano il primo programma informatico (di attribuzione incerta: Babbage o Lovelace?) 

Online si trova moltissimo sulla Lovelace, anche se la sua produzione originale si limitò alla già citata traduzione annotata. Il testo originale di Menabrea può essere scaricato qui, in francese o in italiano, e qui si può leggere la versione della Lovelace, che culmina con la semi-mitica Nota G. 

L'ordine del tempo, di Carlo Rovelli. Cos'è il tempo? Qualcosa che fluisce lentamente, inesorabilmente, continuamente, allo stesso modo ovunque o per chiunque? O qualcosa di locale, soggettivo, confrontabile solo per eventi ravvicinati? Quali fenomeni fisici ne evidenziano il trascorrere, distinguendo il passato dal futuro? Ha senso parlare di "simultaneità" a grandi distanze? Sono questioni profonde, anche dal punto di vista filosofico, alle quali la scienza non ha ancora dato risposte definitive, se mai potrà darle.
Ce ne parla Carlo Rovelli, con il suo consueto stile sempre in equilibrio tra rigore, divulgazione e filosofia, in un libro che mi sento di consigliare senza riserve.