Sfogliando distrattamente, durante una riunione in MS Teams, il primo volume di Mathematical Constants di Steven Finch, mi sono imbattuto nel denesting (simpatica espressione) di Srinivasa Ramanujan
$$
\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}=\frac{1}{3}\left( \sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}\right) \;.
$$
La verifica è presto fatta:
Ma come cavolo ci sarà mai arrivato? Ah già, dimenticavo, Namagiri...
La semplificazione dei radicali doppi riveste una certa importanza nell'ambito degli algoritmi per il calcolo simbolico, come fa notare Susan Landau nel saggio Simplification of nested radicals (consultabile qui), dove il problema viene trattato, dal punto di vista algebrico e da quello computazionale, con gli strumenti della Teoria di Galois. Con carta e penna, la questione è tutt'altro che abbordabile, dal momento che non esistono metodi generali per il denesting, ma solo qualche algoritmo ad hoc come quelli raccolti qui da Stan Brown.
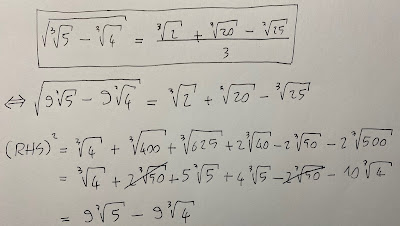
Nessun commento:
Posta un commento