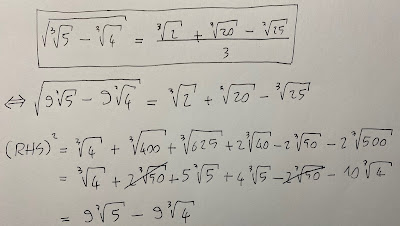Seezza & Quasità

 

Alan Moore non è stato l'unico fumettaro a farsi affascinare dalle "dimensioni aggiuntive". Leggendo la nuova edizione degli Incubi di provincia, raccolta di brevi storie "di nicchia" di quel geniaccio del fumetto che è stato Franco Bonvicini alias Bonvi (ricordate? Le Sturmtruppen, Nick Carter, le Cronache del dopobomba, le Storie dello spazio profondo, Cattivik, Marzolino Tarantola) mi sono imbattuto nel racconto Seezza della Quasità, dove il fortuito ripiegamento di una sorta di origami (come quello della casa nuova di Heinlein) origina uno squarcio nello spaziotempo che avrà conseguenze inimmaginabili per l'intero genere umano. Seezza e Quasità sono i nomi attribuiti alla quarta e alla quinta dimensione, dopo altezza, lunghezza e larghezza.
Bonvi attribuisce l'idea originale a un certo W. S. Trevis, di cui inizialmente non ho trovato traccia online. In realtà si tratta di Walter Stone Tevis, autore americano il cui romanzo forse più famoso, The Queen's Gambit è stato recentemente (ben) trasposto da Netflix nella miniserie La regina degli scacchi (ma ha scritto pure L'uomo che cadde sulla terra,  Lo spaccone e il seguito Il colore dei soldi). Del racconto originale, The Ifth of Oofth, pubblicato nell'aprile del 1957 su Galaxy Science Fiction, Bonvi mantiene l'idea originale, in un'ambientazione un po' più "calda", dove gli insipidi protagonisti sono rimpiazzati dal biondo alter ego dell'autore e dall'Enrichetta, anzi Giovanna, di turno.

Che c'entra il 239?

Anche questa l'ho (ri-)scoperta su Mathematical Constants, Vol. 1:
$$
4\,{\rm arctan}\left(\frac{1}{5}\right)-{\rm arctan}\left(\frac{1}{239}\right)=\frac{\pi}{4}\;.
$$
La verifica, come dicono gli inglesi, è straightforward: essenzialmente, è sufficiente applicare tre volte la formula di addizione per la tangente "rivoltata":

Si tratta della formula che John Machin utilizzò per calcolare le prime cento cifre di $\pi$, sfruttando lo sviluppo in serie di potenza dell'arcotangente (qualche informazione supplementare può essere trovata a questo link).

Ma come avrà fatto?

Sfogliando distrattamente, durante una riunione in MS Teams, il primo volume di Mathematical Constants di Steven Finch, mi sono imbattuto nel denesting (simpatica espressione) di Srinivasa Ramanujan
$$
\sqrt{\sqrt[3]{5}-\sqrt[3]{4}}=\frac{1}{3}\left( \sqrt[3]{2}+\sqrt[3]{20}-\sqrt[3]{25}\right) \;.
$$
La verifica è presto fatta:

Ma come cavolo ci sarà mai arrivato? Ah già, dimenticavo, Namagiri...

La semplificazione dei radicali doppi riveste una certa importanza nell'ambito degli algoritmi per il calcolo simbolico, come fa notare Susan Landau nel saggio Simplification of nested radicals (consultabile qui), dove il problema viene trattato, dal punto di vista algebrico e da quello computazionale, con gli strumenti della Teoria di Galois. Con carta e penna, la questione è tutt'altro che abbordabile, dal momento che non esistono metodi generali per il denesting, ma solo qualche algoritmo ad hoc come quelli raccolti qui da Stan Brown.

Fisica, moderna ma già vintage

Come sappiamo, Albert Einstein sviluppò le sue rivoluzionarie teorie soprattutto nei primi decenni del XX secolo. In particolare (ma assolutamente non solo), la Relatività ristretta vide la luce nel corso dell'annus mirabilis 1905, mentre i fondamenti della Relatività generale furono sviluppati tra il 1907 e il 1915.
Risalgono già a quegli anni i primi, pionieristici tentativi di popolarizzare una teoria che decisamente cozzava con la percezione "newtoniana" dell'universo, con i suoi paradossi, la dilatazione del tempo, la luce che si incurva in prossimità delle stelle.
Anche la nascente industria cinematografica iniziava allora ad esplorare la possibilità di dare il suo contributo all'ampliamento della cultura scientifica, con i primi, pionieristici tentativi di sfruttare "effetti speciali" e animazione per raggiungere un pubblico più vasto di quello che si documentava sui libri.
Fu, nel 1922, il cineasta tedesco Hanns Walter Kornblum il primo a produrre un documentario dedicato alla fisica di Einstein. Intitolato  Die Grundlagen der Einsteinschen Relativitätstheorie, fu presentato alla Fiera di Francoforte, con un buon successo di pubblico. Il film, come moltissime altre opere dell'epoca, è purtroppo andato perso; se ne trova però una descrizione abbastanza dettagliata in un paper pubblicato nel 2009 dalla storica della scienza Milena Wazeck, scaricabile da questo link. Parte di esso sopravvive inoltre all'interno di un altra fondamentale opera dell'epoca, The Einstein Theory of Relativity, cortometraggio prodotto nel 1923 dagli studi di animazione Fleischer (celebri per Betty Boop, Popeye e per la prima versione animata di Superman), in collaborazione con Garrett Putnam Serviss, astronomo e pioniere della divulgazione scientifica (nonché autore di SF). Il film accompagnò l'uscita dell'omonimo libro di Serviss, scansionato e leggibile a questo indirizzo.

Ma eccolo, il film. Un vero e proprio tuffo nel passato, in un'epoca in cui i miei nonni erano bambini o poco più. Fa di sicuro un certo effetto pensarci...